Have you ever wondered what comes after trillion? The concept of large numbers can be fascinating yet overwhelming. Understanding these numbers is essential, especially in fields like finance, science, and technology where dealing with astronomical figures is common. In this article, we will explore the numbers that come after trillion and their significance in various contexts.
As humanity advances, the need for understanding larger numbers becomes increasingly important. From national debts to interstellar distances, large numbers play a critical role in shaping our comprehension of the world and beyond. In this article, we will delve into the sequence of numbers that follow trillion and explore how they are used in real-world applications.
Whether you're a student, a professional, or simply someone curious about mathematics, this article will provide valuable insights into what lies beyond trillion. Let's embark on this journey to unravel the mysteries of large numbers!
Table of Contents
- What Comes After Trillion?
- The Number System Beyond Trillion
- Understanding Scientific Notation
- Real-World Applications of Large Numbers
- A Brief History of Large Numbers
- Long Scale vs Short Scale
- The Mathematical Significance of Large Numbers
- Examples of Large Numbers in Everyday Life
- Frequently Asked Questions
- Conclusion and Call to Action
What Comes After Trillion?
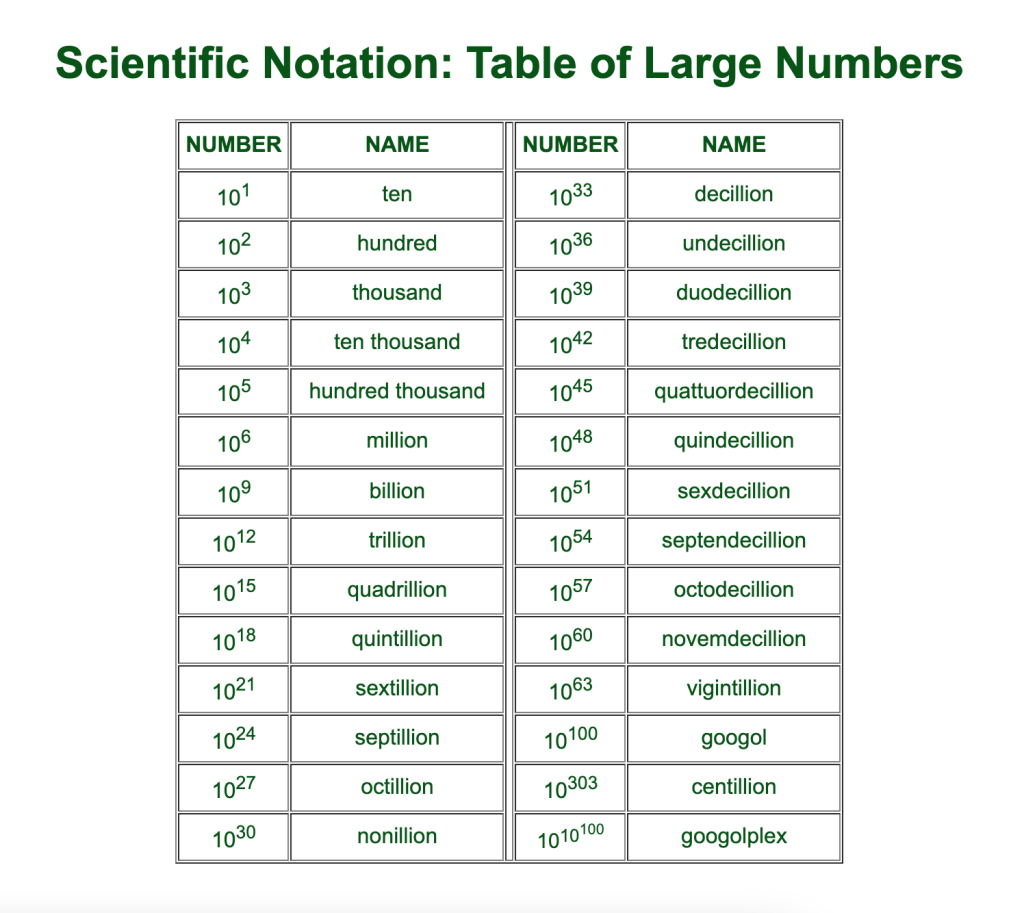
After trillion, the next number in the sequence is quadrillion. In the short scale system used predominantly in the United States, United Kingdom, and many other countries, a quadrillion is represented as \(10^{15}\). This means it is a 1 followed by 15 zeros. In the long scale system, used in some European countries, quadrillion is \(10^{24}\), which is a 1 followed by 24 zeros.
Understanding what comes after trillion is crucial for grasping the magnitude of large numbers. As we move beyond trillion, each subsequent number increases exponentially, making it challenging to comprehend without proper context. Let's explore the sequence further.
Numbers Beyond Quadrillion
Following quadrillion, the sequence continues with quintillion, sextillion, septillion, and so on. Each of these numbers represents an increase in magnitude by a factor of \(10^3\) in the short scale system. For example:
- Quintillion: \(10^{18}\)
- Sextillion: \(10^{21}\)
- Septillion: \(10^{24}\)
These numbers are often used in scientific calculations, financial reports, and astronomical measurements. Their significance lies in their ability to represent vast quantities that are otherwise difficult to conceptualize.
The Number System Beyond Trillion
The number system extends far beyond trillion, with each new term representing an exponential increase in value. The short scale and long scale systems differ in how they define these large numbers, but both are essential for understanding their magnitude.
Short Scale vs Long Scale
The short scale system defines a billion as \(10^9\) and a trillion as \(10^{12}\). In contrast, the long scale system defines a billion as \(10^{12}\) and a trillion as \(10^{18}\). This difference in definition can lead to confusion when interpreting large numbers across different regions.
For example, in the short scale system:
- Quadrillion: \(10^{15}\)
- Quintillion: \(10^{18}\)
While in the long scale system:
- Quadrillion: \(10^{24}\)
- Quintillion: \(10^{30}\)
Understanding the distinction between these systems is vital for accurate communication and interpretation of large numbers.
Understanding Scientific Notation
Scientific notation is a convenient way to represent very large or very small numbers. In scientific notation, numbers are expressed as a product of a decimal number and a power of ten. For example, \(10^{12}\) is written as \(1 \times 10^{12}\).
This notation simplifies the representation of large numbers and is widely used in scientific and mathematical contexts. It allows for easier comparison and manipulation of numbers that would otherwise be cumbersome to write out in full.
Applications of Scientific Notation
Scientific notation is used in various fields, including:
- Astronomy: To measure distances between celestial bodies.
- Physics: To calculate the speed of light and other physical constants.
- Economics: To represent national debts and other large financial figures.
By utilizing scientific notation, scientists and mathematicians can efficiently work with large numbers without losing precision or clarity.
Real-World Applications of Large Numbers
Large numbers are not just abstract concepts; they have practical applications in various aspects of life. From measuring the universe to calculating economic indicators, large numbers play a crucial role in modern society.
Examples in Science
In astronomy, the distance between stars and galaxies is often expressed in light-years, which involves extremely large numbers. For instance, the Andromeda Galaxy is approximately 2.537 million light-years away from Earth, a figure that requires the use of large numbers to accurately represent.
Examples in Finance
National debts and global economic indicators frequently involve numbers beyond trillion. For example, the United States national debt surpassed \(30\) trillion dollars in recent years, highlighting the importance of understanding large numbers in financial contexts.
A Brief History of Large Numbers
The concept of large numbers has fascinated humans for centuries. Ancient civilizations, such as the Greeks and Indians, developed systems to represent large numbers, laying the foundation for modern mathematics.
Archimedes, a renowned Greek mathematician, explored the idea of large numbers in his work "The Sand Reckoner," where he calculated the number of grains of sand that could fit in the universe. This early exploration of large numbers demonstrates humanity's longstanding curiosity about the infinite.
Modern Developments
In modern times, the development of computers and advanced mathematical theories has expanded our ability to work with large numbers. The invention of scientific notation and the use of computers have made it possible to perform calculations involving numbers far beyond what was previously conceivable.
Long Scale vs Short Scale
The distinction between the long scale and short scale systems is an important consideration when dealing with large numbers. While the short scale is predominantly used in English-speaking countries, the long scale is still prevalent in some European nations.
This difference in terminology can lead to misunderstandings, especially in international contexts. For example, a billion in the short scale system is \(10^9\), while in the long scale system, it is \(10^{12}\). Recognizing these differences is essential for accurate communication.
Why the Difference Matters
The difference between the two systems matters in fields such as finance, science, and international trade, where precise communication is crucial. Misinterpretation of large numbers can lead to significant errors, making it vital to clarify which system is being used in any given context.
The Mathematical Significance of Large Numbers
Large numbers hold significant mathematical importance, serving as the foundation for many advanced theories and applications. They are used in fields such as combinatorics, number theory, and cryptography, where their properties are studied and applied.
Applications in Cryptography
In cryptography, large prime numbers are used to create secure encryption algorithms. The difficulty of factoring large numbers is what makes these algorithms secure, ensuring the protection of sensitive information in digital communications.
Understanding the mathematical significance of large numbers is essential for anyone working in fields that rely on advanced mathematical concepts.
Examples of Large Numbers in Everyday Life
While large numbers may seem abstract, they have practical applications in everyday life. From measuring the size of the universe to calculating the number of cells in the human body, large numbers are integral to our understanding of the world.
Everyday Examples
- The estimated number of stars in the observable universe is around \(2 \times 10^{24}\).
- The human body contains approximately \(37.2 \times 10^{12}\) cells.
- The global internet traffic in 2023 was estimated to exceed \(4 zettabytes\), which is \(4 \times 10^{21}\) bytes.
These examples demonstrate how large numbers are used to quantify and understand the vastness of the world around us.
Frequently Asked Questions
1. What Comes After Trillion?
After trillion, the next number in the sequence is quadrillion, followed by quintillion, sextillion, and so on.
2. Why Are Large Numbers Important?
Large numbers are important for accurately representing and understanding vast quantities in fields such as science, finance, and technology.
3. What Is the Difference Between Short Scale and Long Scale?
The short scale and long scale systems differ in how they define large numbers, with the short scale being predominantly used in English-speaking countries and the long scale in some European nations.
4. How Are Large Numbers Used in Science?
Large numbers are used in science to measure distances, calculate physical constants, and represent astronomical data.
Conclusion and Call to Action
In conclusion, understanding what comes after trillion and the significance of large numbers is essential for anyone interested in mathematics, science, or finance. From measuring the universe to calculating economic indicators, large numbers play a crucial role in shaping our understanding of the world.
We invite you to share your thoughts and questions in the comments section below. Additionally, explore other articles on our site to deepen your knowledge of various topics. Together, let's continue to explore the fascinating world of numbers and their applications!
Sources:
- Scientific American
- National Aeronautics and Space Administration (NASA)
- United States Census Bureau